|
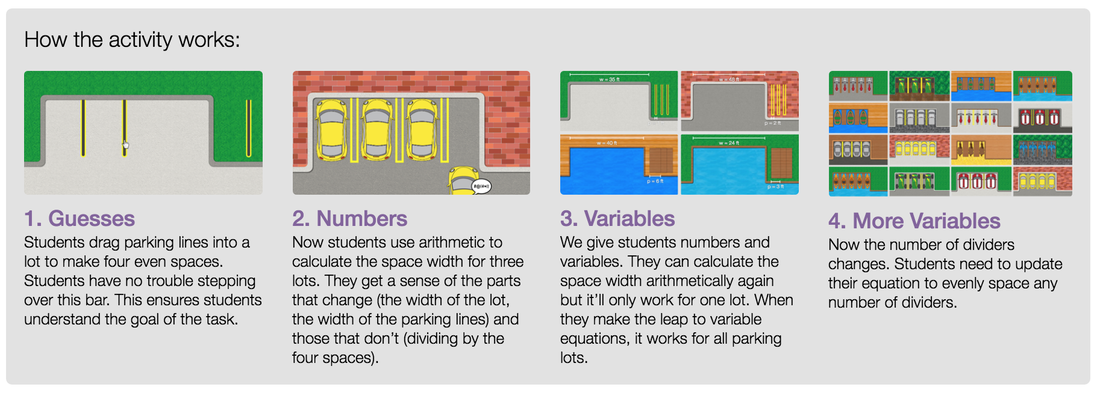
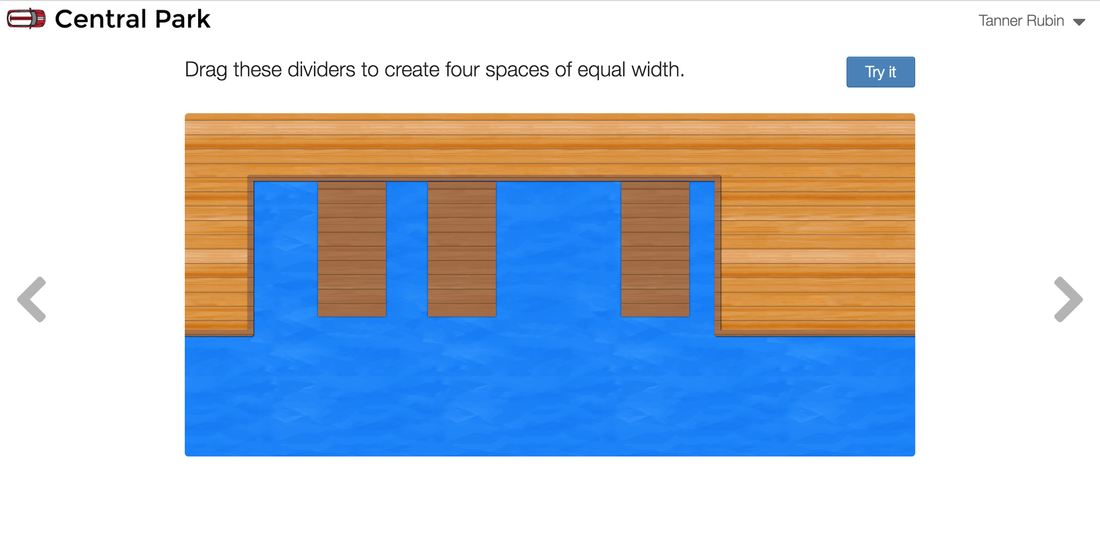
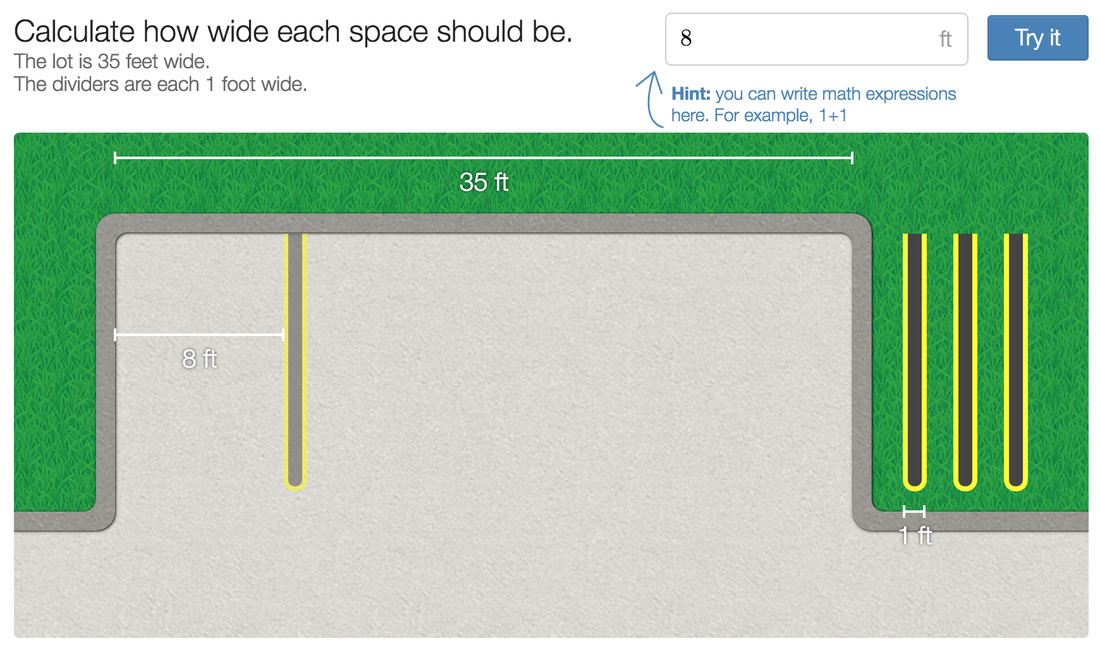
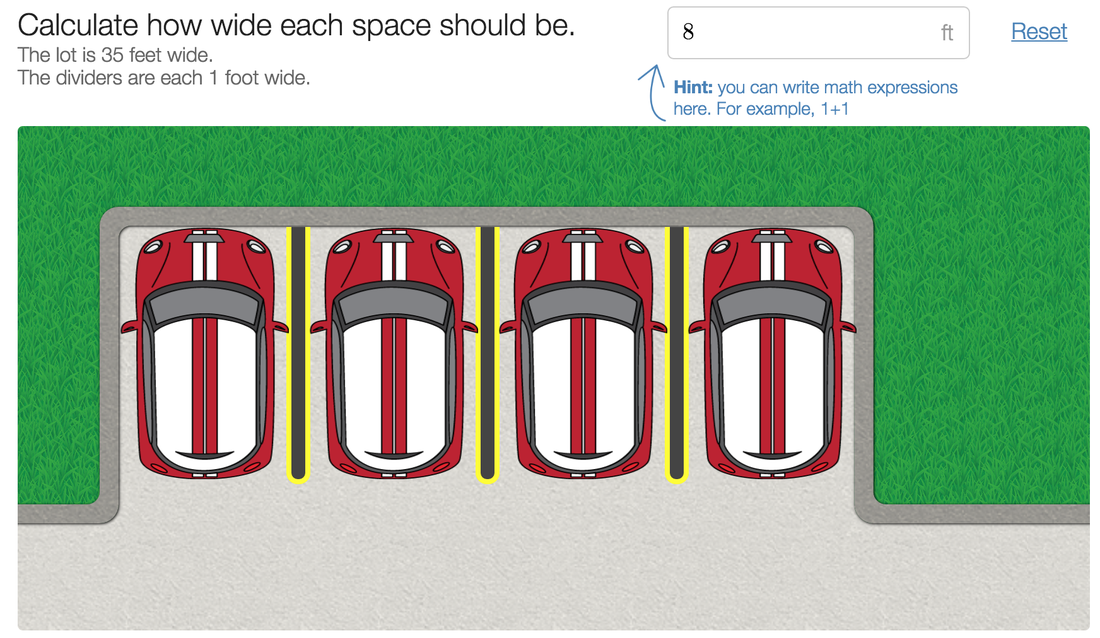
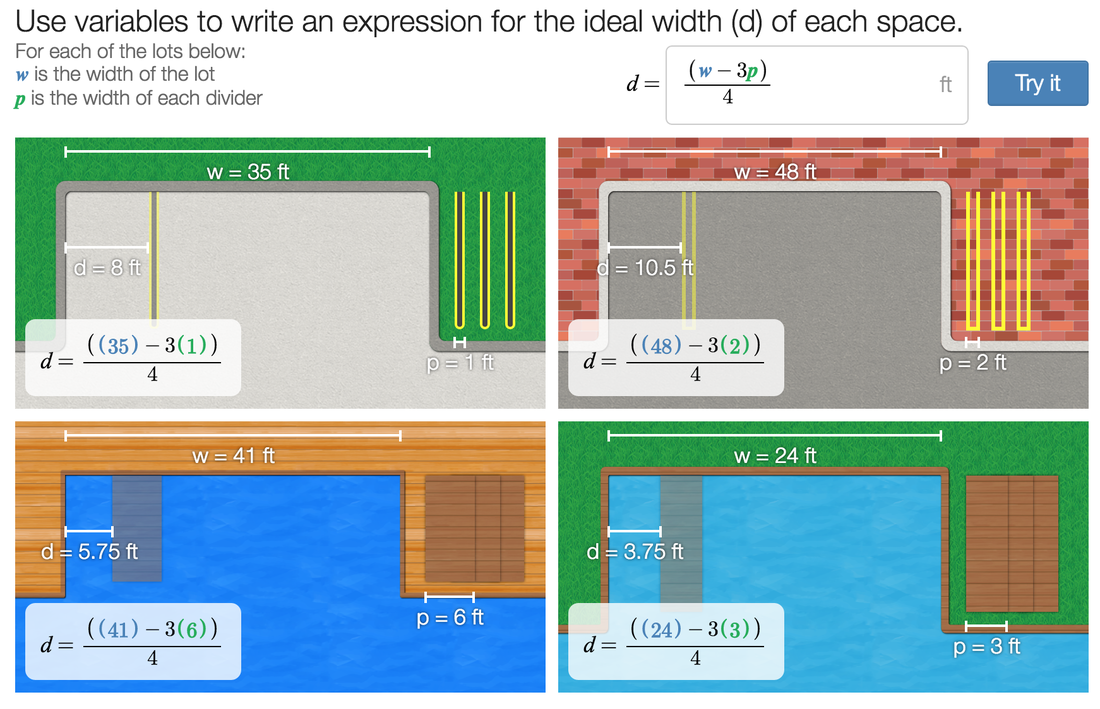
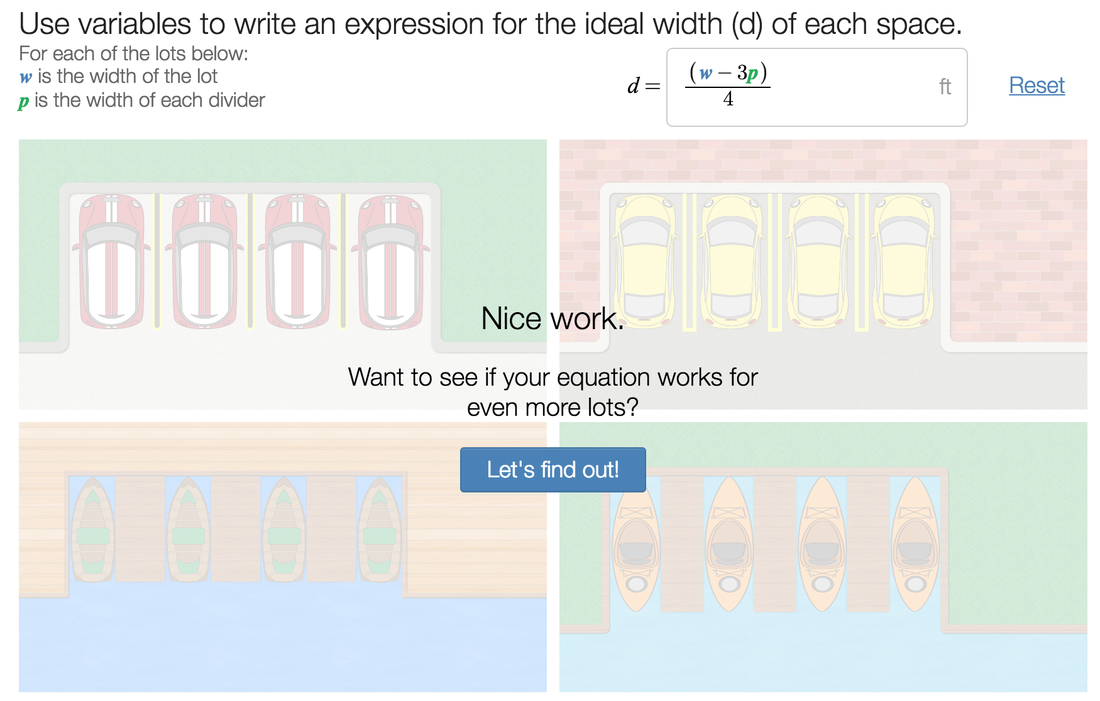
My favorite show of all time with no question about it is Friends. I have watched those episodes probably an unhealthy amount of times, and they're somehow still funny to me! This is a math blog though, so how does Friends have anything to do with math? Well, Friends itself doesn't at all, but as I was exploring teacher.desmos.com for various classroom learning activities, I stumbled across one called "Central Park" (https://teacher.desmos.com/centralpark), which led me to think about New York City, which led me to start thinking about Friends. So, as much of a stretch as that probably is, I likely have your attention now if you're still reading, don't I? Desmos, for those of you readers who don't know, is a combination of many things: a website, an online classroom activity source, a place to turn in work, or in other words, a math teacher's heaven. What I'm setting out to achieve as you read this today is not only to help you explore what a specific teacher.desmos.com activity would look like to use with students, but hopefully in the process, convince you to integrate Desmos or another technological source in your teaching as well. "Central Park" is a Desmos activity that has students "use their knowledge of computation to inform their algebra understanding, and...see that representing their ideas with algebra can save a lot of computation time," or in other words, convince students of their need for algebra to do arithmetic more efficiently. Through the activity, they will be designing parking lots for various cars, first only visually, then slowly integrating numbers and mathematic concepts to help them understand the transition. Almost every Desmos activity will have a "how the activity works" section, or something similar (as pictured below). So let's go through the activity, and try to experience it as students would. First, we simply guess what the spaces should look like, no numbers included. This allows students to develop a practical understanding of a situation before adding numbers, which may be overwhelming before they understand why the numbers are there. Students can then "try it" to see if they were successful in their setup or not! Next up: adding numbers. This is where you take the basis of understanding these students have for a hypothetical situation, and apply mathematics practically, thus demolishing the ever present student question "when am I ever going to use this?" The order of these is integral: helping them understand the need, then giving them the solution. The students now get a chance to calculate how wide the spaces need to be to fit the cars instead of just guessing. They will see through this that we are giving them a much more efficient method, even though it is not what they are used to! Below are some examples of this in the activity. We have them in our grip, now! They love the numbers! Now, we transition into variables, help them understand how those will help, then tell them they have begun doing algebra. Before they know it, algebra has become something they are excited to use instead of such a daunting word! Below are a couple more pictures of how "Central Park" transitions this in the activity. Then dive in and experiment with even more variables... Almost as if by magic, just 45 minutes later, you have a full classroom of students excited about algebra. Unheard of! Although this obviously isn't foolproof in every single classroom, hopefully I have convinced you that it will at least help, and definitely not hurt students' learning. If you have any thoughts on this activity, or Desmos in general, please feel free to comment below and let me know! I'm open to thoughts, and I'd love to hear what has worked (or not worked) for you. And as always, be on the lookout for what comes next from my thoughts outside the glass tank.
5 Comments
Why am I looking in from outside a glass tank? Well, not exactly a tank, but it sure felt that way. I once had a classroom with so many windows that I felt like people were always observing me during class from the outside of the room. For some reason, that's the image I have set in my head as a classroom. When I think classroom, that's what comes to mind. So as MTH 229 begins and I dive into thoughts and ideas on teaching methods and approaches, I have resolved to process my thoughts observing from outside the glass tank in writing. Here we go!
Coming into Math 229, I didn't know much of what to expect. "Mathematical Activities for Secondary Teachers," it was called. That could really mean anything within the realm of high school teaching. From day 1 of the class, it was evident that this was no traditional math class. We began by circling around the classroom, and doing a counting activity. Yeah, one that they might do in a 3rd grade classroom...but we were a classroom full of college students. A profound concept came from such a simple activity though: as we dissected the different ways students were calculating what the, say, 12th number in the sequence would be, there were at least 4 or 5 different ways of getting that 12th number that we came up with. A takeaway from this activity: sometimes we don't understand the purpose until we've accomplished the task. Even more importantly, the concept of the multiple method approach began to take root in my mind. Throughout these first 3 days of class, the central message I have taken away and understood more deeply each time has been encouraging multiple correct ways to approach a problem and celebrating the diversity of problem solving skills. My understanding of how mathematics works has already been challenged, and I'm forced to think about the question Dan Meyer proposes and answers: Does math class need a makeover?
After watching Dan passionately attest to why he believes mathematics is being taught poorly in some situations, I realize how much I agree with him. He states five symptoms that math is being taught wrongly, which you can see in his TED talk above, but I will focus on one that I've seen very presently and agree strongly with. When math is being taught poorly, there is a clear lack of retention. Almost every time I take a math class that references something I learned more than a year in the past, I have to, to an extent, re-learn the ideas. Then I think about how different my past classes have approached teaching to how I am learning in this class. None of those classes focused on how I got to the answer, but rather that I got the answer. Already I see myself analyzing math problems differently when I look at the method. In agreement with Dan, encouraging student intuition, letting them build the problem, and allowing them to explore different methods of solving are clearly most effective of the methods of teaching.
Whew. Those we're some thoughts. To close out this post, I'd love to talk about some of the specifics from Math 229 so far. As we explore resources for teachers, Desmos (https://www.desmos.com/) has been a very intriguing program. A free calculator online, with seemingly endless possibilities. Any teacher who loves exploring new ways to use technology would feel like a kid in a candy store discovering this program. With all sorts of graphing methods and animations available, it can be used basically as a free online graphing calculator. That alone is fantastic, but the way teachers can use it is even better. You can create groups where you propose a question and actually get to see how students are approaching answering that question as their graphs and attempts pop up on your screen. Once again, that theme of encouraging students to approach problem solving in different ways returns. Finally, let's take a look at some of the topics of conversation revolving around quadratic functions from day 3 of MTH 229. I'd be surprised if you didn't know about the controversy surrounding the infamous Common Core (CC) Standards. During class, we took some time to delve into these standards and understand a little more about what the CC is, taking the example of the standards for quadratic functions. A conclusion I have come to is that the standards on the Common Core website (http://www.corestandards.org/) seem fair, but also seem very unclear. I understand why people are initially scared of them. For example, CCSS.MATH.CONTENT.HSF.LE.A.2 is written as "Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table)" (See http://www.corestandards.org/Math/Content/HSF/LE/). Initially this does seem a little unclear, but as I translated it more simply to "I can construct linear and exponential functions given various parts of the problem," it seems a little more straightforward. That of course is just one example. I will form more of an opinion as I learn more about the Common Core Standards, but with just some basic knowledge of the quadratic function standards for example, they don't seem too bad. Don't quote me on that quite yet, though, I haven't yet tried all the approaches of understanding their use and purpose yet... Thanks for reading, and be ready for more thoughts as I continue to learn about what teaching looks like from outside the glass tank. |
AuthorWrite something about yourself. No need to be fancy, just an overview. ArchivesCategories |



 RSS Feed
RSS Feed
